Question

Find the area of the shaded region. enter a decimal rounded to the nearest tenth

Answer 1

73.6

Explanation:

Answer 2

78.42

Explanation:

Area of 360 - 80 degree region.

You need to find out the region of the major arc where the circle is almost complete. The area left over will be calculated later

Angle = 360 -80

Angle = 280 degrees.

Area =
`(angle*3.14*r^2)/(360)`

Area =
`(280*3.14*5^2)/(360)`

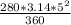
Area = 23800/360

Area = 66.11

Area of the Triangle with sides of 5 cm each

Here's where I get into a bit of trouble. I have to assume you know some trig.

Find the height

Cos(40) = The height / the hypotenuse

Cos(40) = h/5

0.7760 = h/5

h = 0.7760*5

h = 3.830

Find 1/2 the base (the chord of the circle)

Sin(40) = 1/2 base / hypotenuse

Sin(40) = 1/2 b / 5 Multiply both sides by 5

1/2 b = 5*sin(40) Find the sin(40)

1/2 b = 5*.6428 Combine the right

1/2 b = 3.139 multiply by 2

b = 6.4278

Find the area of the triangle

Area = 1/2 b * h

b = 6.4278

h = 3.830

Area = 1/2 * 6.4278*3.830

Area = 12.31 cm^2

Total Area

12.31 + 66.11 = 78.42