Answer:
-1.32
Explanation:
Since we want to test if
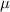 of the alternative hypothesis is less than the established in the null, this is a left-tailed test.
of the alternative hypothesis is less than the established in the null, this is a left-tailed test.
At 10% significance level the t-statistic (t-value) is the value of t such that the area under the Student's t-distribution curve with 25 degrees of freedom (sample size -1) to the left of t equals 10% = 0.1
Either by using a table or the computer, we find
