Question

Edward is making a rectangular picture frame. He wants the perimeter of a frame to be no more than 96 inches. He also wants the length of the frame to be greater than or equal to the square of 4 inches less than its width.

Instructions: Create a system of inequalities tomorrow love you both situation and use it to determine how many of the solutions are viable.

Answer 1

No more than in terms of math means less than or equal to.

P = 2l + 2w

{96 ≤ 2l + 2w

{L ≥ w - 4

Here we see a system of linear inequality in two variables.

You finish.

Answer 2

A system of inequalities to model the situation is 2l + 2w ≤ 96 and
`l\geq w-4^(2)`.

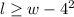The number of solutions that are viable is: C. Part of the solution region includes a negative width; therefore, not all solutions are viable for the given situation.

In Mathematics and Geometry, the perimeter of a rectangle can be calculated by using this mathematical equation (formula);

P = 2(l + w) or P = 2l + 2w

Where:

• P represent the perimeter of a rectangle.
• w represent the width of a rectangle.
• l represent the length of a rectangle.

Since Edward wants the perimeter of a frame to be no more than 96 inches, an inequality to model the situation is given by;

2l + 2w ≤ 96.

Additionally, Edward wants the length of the frame to be greater than or equal to the square of 4 inches less than its width;

`l\geq w-4^(2)`

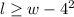
By solving the system of inequalities, a set of viable solutions include;

(20, 10), (30,0), (20, 0), (30, 10), (10, 10).

In concluson, part of the solution region includes a negative width, so, it is not all solutions that are viable for the given situation.

Complete Question:

Edward is making a rectangular picture frame. He wants the perimeter of the frame to be no more than 96 inches. He also wants the length of the frame to be greater than or equal to the square of inches less than its width.

Create a system of inequalities to model the above situation and use it to determine how many of the solutions are viable.

Part of the solution region includes a negative length; therefore, not all solutions are viable for the given situation.

The entire solution region is not viable.

Part of the solution region includes a negative width; therefore, not all solutions are viable for the given situation.

No part of the solution region is viable because the length or width cannot be negative.

The entire solution region is viable