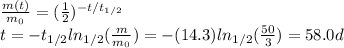Question

4. Phosphorus-32 has a half-life of 14.3days. How long would it take a 50-mg sample to decay to 3 mg

Answer 1

58.0 days

Explanation:

The equation for the radioactive decay is

`m(t)=m_0 ((1)/(2))^{-t/t_(1/2)}`

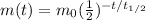
where

m(t) is the mass of the sample left at time t

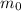`m_0` is the initial mass of the sample

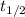`t_(1/2)` is the half-life

For the phosporus-32 isotope in the problem, we have:

`t_(1/2)=14.3 d` (half-life in days)

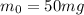`m_0 = 50 mg` is the initial mass

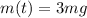`m(t)=3 mg` is the mass at time t

Solving for t, we find the time needed for the sample to reduce to 3 mg:

`(m(t))/(m_0) = ((1)/(2))^{-t/t_(1/2)}\\t=-t_(1/2) ln_(1/2) ((m)/(m_0))=-(14.3) ln_(1/2) ((50)/(3))=58.0 d`