Question

A shell is fired from the ground with the initial speed of 1570 m/s at an initial angle of 41 to the horizontal.

Neglecting air resistance, find the shell's horizontal range.

Answer 1

`2.49\cdot 10^5 m`

Step-by-step explanation:

The horizontal range of a projectile is given by

`d=(u^2 sin 2\theta)/(g)`

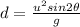
where

u is the initial speed

`\theta` is the angle of launch

g = 9.8 m/s^2 is the acceleration of gravity

For the shell in this problem,

u = 1570 m/s

`\theta=41^(\circ)`

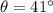
Substituting into the equation, we find the range of the shell:

`d=((1570)^2)/(9.8) sin (2\cdot 41)=2.49\cdot 10^5 m`