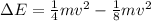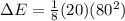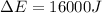Answer:
Part a)
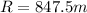
Part b)
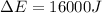
Step-by-step explanation:
As we know that projectile is launched at an angle of 60 degree with the horizontal
so at highest point of its path the velocity of projectile is only along horizontal direction
so we will have
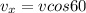
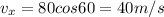
now it explodes into two equal parts so by momentum conservation we will have
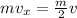

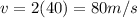
Part a)
time of flight of the projectile is given as
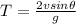
now total distance moved by it is given as

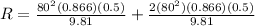
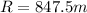
Part b)
Energy released = change in kinetic energy