Question

(b) After how many complete years will a starting capital of RM5 000 first exceed RM10 000 if it grows at 6% per annum?

Answer 1

The capital will first exceed RM 10 000 after 12 complete years.

Explanation:

This is a compound interest problem.

The compound interest formula is given by:

`A = P(1 + (r)/(n))^(nt)`

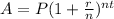
Where A is the amount of money, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per unit t and t is the time the money is invested or borrowed for.

In this exercise, we have:

So, for our problem, we have:

We first want to find t, when
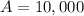`A = 10,000`, given that
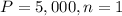`P = 5,000, n = 1` and
`r = 0.06`.

`A = P(1 + (r)/(n))^(nt)`

`10,000 = 5,000(1 + (0.06)/(1))^(t)`

`1.06^(t) = 2`

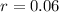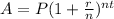
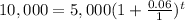
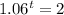
Now we apply log to both sides. Important to remember the following proprierty:

`\log{a^(b)} = b\log{a}`

`\log{1.06^(t)} = \log{2}`

`t\log{1.06} = \log{2}`

`t = \frac{\log{2}}{\log{1.06}}`

`t = 11.9`

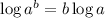
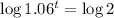
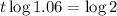
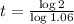
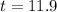
11.9 years is 11 years and some 330 days. The next complete year will be the 12th year.

The capital will first exceed RM 10 000 after 12 complete years.