Question

The Census Bureau reports that 82% of Americans over the age of 25 are high school graduates. A survey of randomly selected residents of a certain county included 1210 who were over the age of 25, and 1030 of them were high school graduates.

(a) Find the mean and standard deviation for the number of high school graduates in groups of 1210 Americans over the age of 25.

Mean =

Standard deviation =

(b) Is that county result of 1030 unusually high, or low, or neither? (Enter HIGH or LOW or NEITHER)

Answer 1

a) Mean = 1030; Standard deviation = 12.38.

b) The county result is unusually high.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X. Subtracting 1 by the pvalue, we This p-value is the probability that the value of the measure is greater than X.

(a) Find the mean and standard deviation for the number of high school graduates in groups of 1210 Americans over the age of 25.

This first question is a binomial propability distribution.

We have a sample of 1210 Amricans, so
`n = 1210`.

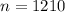The mean of the sample is 1030.

The probability of a success is
`\pi = (1030)/(1210) = 0.8512`.

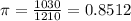The standard deviation of the sample is
`s = √(n\pi(1-\pi)) = √(1210*0.8512*0.1488) = 12.38`

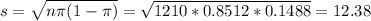
(b) Is that county result of 1030 unusually high, or low, or neither?

The first step is find the zscore when
`X = 1030`.

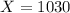Then we find the pvalue of this zscore.

If this pvalue is bigger than 0.95, the county result is unusually high.

If this pvalue is smaller than 0.05, the county result is unusually low.

Otherwise, it is neither.

The national mean is 82%. So,

`\mu = 0.82(1210) = 992.2`

`Z = (X - \mu)/(\sigma)`

`Z = (1030 - 992.2)/(12.38)`

`Z = 3.05`

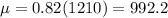
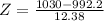
`Z = 3.05` has a pvalue of 0.9989.This means that the county result is unusually high.