Question

A car insurance company has determined that 8% of all drivers were involved in a car accident last year. Among the 15 drivers living on one particular street, 3 were involved in a car accident last year. If 15 drivers are randomly selected, what is the probability of getting 3 or more who were involved in a car accident last year?

Answer 1

There is an 11.3% probability of getting 3 or more who were involved in a car accident last year.

Explanation:

For each driver surveyed, there are only two possible outcomes. Either they were involved in a car accident last year, or they were not. This means that we solve this problem using binomial probability concepts.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

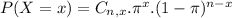
In which
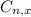`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

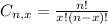
And
`\pi` is the probability of X happening.

In this problem

15 drivers are randomly selected, so
`n = 15`.

A success consists in finding a driver that was involved in an accident. A car insurance company has determined that 8% of all drivers were involved in a car accident last year. This means that
`\pi = 0.08`.

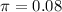What is the probability of getting 3 or more who were involved in a car accident last year?

This is
`P(X \geq 3)`.

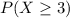Either less than 3 were involved in a car accident, or 3 or more were. Each one has it's probabilities. The sum of these probabilities is decimal 1. So:

`P(X < 3) + P(X \geq 3) = 1`

`P(X \geq 3) = 1 - P(X < 3)`

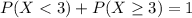
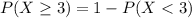
In which

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)`

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

`P(X = 0) = C_(15,0).(0.08)^(0).(0.92)^(15) = 0.2863`

`P(X = 1) = C_(15,1).(0.08)^(1).(0.92)^(14) = 0.3734`

`P(X = 2) = C_(15,2).(0.08)^(2).(0.92)^(13) = 0.2273`

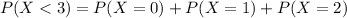
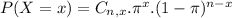
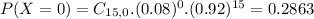
So

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.2863 + 0.3734 + 0.2273 = 0.887`

Finally

`P(X \geq 3) = 1 - P(X < 3) = 1 - 0.887 = 0.113`

There is an 11.3% probability of getting 3 or more who were involved in a car accident last year.