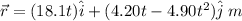Question

A golf ball is hit off a tee at the edge of a cliff. Its x and y coordinates as functions of time are given by x = 18.1t and y = 4.20t − 4.90t2, where x and y are in meters and t is in seconds. (a) Write a vector expression for the ball's position as a function of time, using the unit vectors î and ĵ. (Give the answer in terms of t.)

Answer 1

The vector for the ball’s position is
`\vec{r} = (18.1t)\hat{i} + (4.20t - 4.90t^2)\hat{j} \:m`

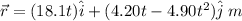
Explanation:

The position vector for a particle moving in the x-y plane can be written

`\vec{r} = x\hat{i} + y\hat{j}`

where x, y, and
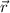`\vec{r}` change with time as the particle moves while the unit vectors
`\hat{i}` and
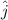`\hat{j}` remain constant.

We know that the x and y coordinates as functions of time are given by
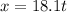`x = 18.1t` and
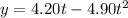`y = 4.20t - 4.90t^2`, where x and y are in meters and t is in seconds.

Therefore, the vector for the ball’s position is
`\vec{r} = (18.1t)\hat{i} + (4.20t - 4.90t^2)\hat{j} \:m`