Question

A high school basketball court measures 84 feet by 50 feet. If a coach has her players sprint diagonally across the court, how far do they run (in feet)?

Answer 1

The players run 97.54 feet in total across the diagonal of the field.

Explanation:

The basket ball is in the figure of a rectangle.

The dimensions of the court are 84 feet by 50 feet.

Now, by PYTHAGORAS THEOREM

in a right angled triangle ABC:

`(base)^(2)  + (height)^(2)  = (hypotenuse)^(2)`

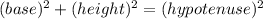
Here, the the basket ball field,

length of basket field = the base of the triangle

width of the field = the height of triangle

Diagonal of the triangle = Hypotenuse of the triangle

So,
`(Width)^(2)  + (height)^(2)  = (Diagonal)^(2)`

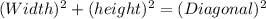
or,
`(84)^(2)  + (50)^(2)   = (D)^(2)`

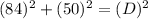
or,
`(D)^(2)  = 7056 + 2500 = 9556\\or, D = √(9556) = 97.54`

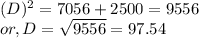
Hence, the length of the diagonal is 97.54 feets

So, the players run 97.54 feet in total across the diagonal of the field.