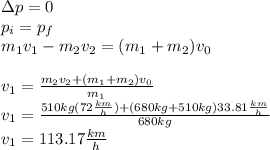Question

You have been called to testify as an expert witness in a trial involving a head-on collision. Car A weighs 680.0 kg and was traveling eastward. Car B weighs 510.0 kg and was traveling westward at 72.0 km/h. The cars locked bumpers and slid eastward with their wheels locked for 6.00 m before stopping. You have measured the coefficient of kinetic friction between the tires and the pavement to be 0.750. 1) How fast (in kilometer per hour) was car A traveling just before the collision? (Express your answer to three significant figures.

Answer 1

`113.17(km)/(h)`

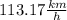
Step-by-step explanation:

In order to know the velocity of the cars after the collision, we must calculate the acceleration after the collision. According to Newton's second law:

`\sum F_x:f_k=ma\\\sum F_y=N-mg=0\\N=mg\\f_k=\mu_k N=\mu_k mg\\a=(f_k)/(m)\\a=(\mu_k mg)/(m)\\a=0.75*9.8(m)/(s^2)\\a=7.35(m)/(s^2)`

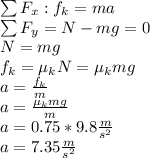
Using the following kinematics equation, we calculate the initial velocity which is the same velocity after collision, so, the final velocity is zero since the cars stopped after 6 meters:

`v_f^2=v_0^2-2ax\\v_0=√(v_f^2+2ax)\\v_0=\sqrt{0^2+2(7.35(m)/(s^2))(6m)}\\v_0=9.39(m)/(s)*(3600s)/(1h)(1km)/(1000m)=33.81(km)/(h)`

According to the law of conservation of momentum and solving for
`v_1`:

`\Delta p=0\\p_i=p_f\\m_1v_1-m_2v_2=(m_1+m_2)v_0\\\\v_1=(m_2v_2+(m_1+m_2)v_0)/(m_1)\\v_1=(510kg(72(km)/(h))+(680kg+510kg)33.81(km)/(h))/(680kg)\\v_1=113.17(km)/(h)`