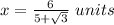Answer:
The height of the right trapezoid is
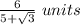
Explanation:
Let
x ----> the height of the right trapezoid in units
we know that
The perimeter of the figure is equal to
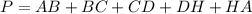
we have
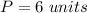
 ---> because is a square
---> because is a square
substitute

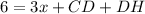 -----> equation A
-----> equation A
In the right triangle CDH
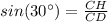
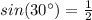
so
Remember that
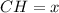
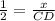

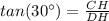
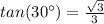
so

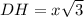
substitute the values in the equation A
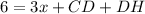 -----> equation A
-----> equation A

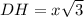
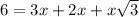
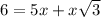
![6=x[5+√(3)]](https://img.qammunity.org/2020/formulas/mathematics/college/8n6dppvcacybz8zjclprqj6l3zsumcry61.png)