Answer:
-39
Explanation:
The expression in this problem is
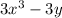
We want to evaluate this expression when

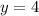
Substituting into the expression, we find:
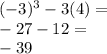
Because
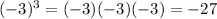
and
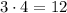
And this expression is a polynomial, which is an expression consisting of more than one algebraic terms (in this case, two of them)