Question

A crop initially has N₀ Bacterias. After 1 hour the crop has reached ( 3/2 ) N₀ Bacterias. If the rapid growth in that crop is proportional to the number bacteria present at the time t, determine the time required for the number of bacterias grouper are tripled.

Answer 1

2.71 hours are required for the number of bacterias grouper are tripled.

Explanation:

The number of bacterias can be given by the following exponential function:

`N(t) = N_(0)e^(rt)`

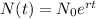
In which
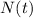`N(t)` is the number of bacterias at the time instant t,
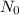`N_(0)` is the initial number of bacterias and r is the rate for which they grow.

After 1 hour the crop has reached ( 3/2 ) N₀ Bacterias.

This means that
`N(1) = 1.5N_(0)`. With this information, we can find r.

`N(t) = N_(0)e^(rt)`

`1.5N_(0) = N_(0)e^(r)`

`e^(r) = 1.5`

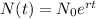
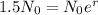
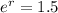
To find r, we apply ln to both sides

`\ln{e^(r)} = ln(1.5)`

`r = 0.405`

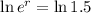
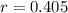
Determine the time required for the number of bacterias grouper are tripled.

This is t when
`N(t) = 3N_(0)`

`N(t) = N_(0)e^(0.405t)`

`3N_(0) = N_(0)e^(0.405t)`

`e^(0.405t) = 3`

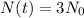
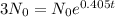
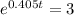
Again, we apply ln to both sides

`\ln{e^(0.405t)} = ln(3)`

`0.405t = 1.10`

`t = 2.71`

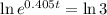
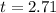
2.71 hours are required for the number of bacterias grouper are tripled.