Question

An airline pilot begins a trip to Duluth from an airport located 1500 km south of Duluth. Her air speed is 260 m/s, but a wind blows from west to east at 40 m/s that takes her off course if she flies directly north. She has the choice of heading slightly westward so that the wind causes her to end up at Duluth or heading due north until she reaches a position directly east of Duluth and then heading west into the wind to Duluth.

Which route takes a shorter time interval?

A) The first route will be shorter.
B) The second route will be shorter.
C) The routes are equal to each other.

Answer 1

A) The first route will be shorter

Step-by-step explanation:

Speed =
`(Distance)/(Time)`

The total distance to be covered in each case is 1500 Km= 1500000 m.

Heading westward, her air speed = 260 m/s.

So that the time required to cover the distance at that speed would be;

Time =
`(Distance)/(Speed)`

=
`(1500000)/(260)`

= 5769.231 seconds

But if she flies directly north, a blowing wind reduces her speed. Thus speed due north,
`S_(N)` is given by;

`S_(N)` =
`\sqrt{260^(2) - 40^(2) }`

= 256.91 m/s

Time for traveling =
`(Distance)/(Speed)`

=
`(1500000)/(256.91)`

= 5838.621 seconds

Thus comparing the time of travel in both cases, the first route would be shorter .

Answer 2

Option A

The first route will be shorter

Step-by-step explanation:

Considering the motion when the airline heads westward, the north direction speed is given by

`N=\sqrt 260^(2)-40^(2)=257 m/s`

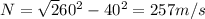
Distance to destination is 1500 Km= 1500000 m

Time for travelling=1500000/257=5836.58 seconds

Time in minutes=5836.58/60=97.3 minutes

In case the wind sends pilot off the course

Time to travel from A to point E before heading to Duluth=1500000/260=5769.23 seconds

Time in minutes=5769.23/60=96.2 minutes

Time to travel from Westward to Duluth=Distance/speed

Distance between Westward and Duluth=40*5769.23=230769.23 m

Time to travel from Westward point to Duluth=23769.23/(260-40)=1048.95 seconds

Time in minutes=1048.95/60=17.5 minutes

Total time taken when pilot changes course=96.2+17.5=113.7 minutes

Time difference=113.7-97.3=16.4 minutes

Therefore, the first route will be shorter .