Question

Three balls are launched from the same point high on a cliff - they all end up landing at different places on the flat ground below. The launch point is 30.0 m above the ground, and all the balls are launched with the same speed of 28.0 m/s. Ball A is launched with an initial velocity that is entirely horizontal. Ball B's initial velocity is directed at an angle of 43.0 degrees above the horizontal. Ball C's initial velocity is directed at an angle of 22.0 degrees below the horizontal. As usual, we will neglect air resistance. Use ​g = 9.80 \; m/s^2​. Rank the balls based on the speed they each have just before impact with the ground, from largest to smallest.

Answer 1

speed ball A = speed ball B = speed ball C = 37.0 m/s

Step-by-step explanation:

The position and velocity vectors of the balls can be calculated using the following equations:

r = (x0 + v0 · t · cos α, y0 + v0 · t ·sin α + 1/2 · g · t²)

v = (v0 · cos α, v0 · sin α + g · t)

Where:

r = position vector at time t.

x0 = initial horizontal position.

v0 = initial velocity.

t = time.

α = launching angle.

y0 = initial vertical position.

g = acceleration due to gravity (-9.80 m/s² considering the upward direction as positive).

v = velocity vector at time t.

First, let´s calculate the time it takes the balls to reach the ground. Let´s place the origin of the frame of reference at the launching point so that x0 and y0 = 0.

At the final time, the y-component of the position vector is -30.0 m. Then, using the equation of the vertical position we can obtain the time it takes the balls to reach the ground:

y = y0 + v0 · t ·sin α + 1/2 · g · t²

At the final time, y = -30 m. Then:

-30.0 m = y0 + v0 · t ·sin α + 1/2 · g · t²

For ball A, the launching angle, α, is 0. The initial position is also 0. Then:

-30.0 m = 28 m/s · t · sin 0° - 1/2 · 9.80 m/s² · t²

-30.0 m = -4.90 m/s² · t²

-30.0 m / -4.90 m/s² = t²

t = 2.47 s

The velocity vector when the ball reaches the ground will be:

v = (vx, vy)

v = (v0 · cos α, v0 · sin α + g · t)

vx = v0 · cos α

vx = 28.0 m/s · cos 0°

vx = 28.0 m/s

vy = v0 · sin 0° -9.80 m/s² · 2.47 s

vy = -24.2 m/s

Then:

v = (28.0 m/s, -24.2 m/s)

The magnitude of the velocity vector is calculated as follows:

`|v| = \sqrt{(28.0 m/s)^(2) + (24.2 m/s)^(2)}=37.0 m/s`

The velocity of ball A when it reaches the ground is 37.0 m/s.

For ball B, we have to follow the same procedure only that α = 43.0°. Then, let´s start calculating the time it takes the ball to reach the ground:

-30.0 m = 28.0 m/s · t · sin 43.0° - 1/2 · 9.80 m/s² · t²

0 = 30.0 m + 28.0 m/s · t · sin 43.0° - 4.90 m/s² · t²

Solving the quadratic equation:

t = 5.10 s (the other solution is discarded because it is negative).

t = 5.098068502 (without rounding)

Then, the velocity will be:

vx = v0 · cos α

vx = 28.0 m/s · cos 43.0°

vx = 20.5 m/s

vy = v0 · sin α + g · t

vy = 28.0 m/s · sin 43.0° -9.80 m/s² · 5.10 s

vy = -30.9 m/s

Then the velocity vector will be:

v = (20.5 m/s, -30.9 m/s)

And its magnitude will be:

`|v| = \sqrt{(20.5 m/s)^(2) + (30.9 m/s)^(2)}=37.1 m/s`

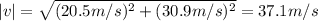
When you do the calculations without rounding any intermediate result, the speed of ball B is equal to the speed of ball A.

The velocity of ball B when it reaches the ground is 37.0 m/s

For ball C, α = 22.0°. Then:

y = v0 · t ·sin α + 1/2 · g · t²

-30.0 m = 28.0 m/s · t · sin 22.0° - 1/2 · 9.80 m/s² · t²

0 = 30.0 m + 28.0 m/s · t · sin 22.0° - 4.90 m/s² · t²

Solving the quadratic equation:

t = 3.77 s

t = 3.766227551 (without rounding)

The velocity will be:

vx = v0 · cos α

vx = 28.0 m/s · cos 22.0°

vx = 26.0 m/s

vy = v0 · sin α + g · t

vy = 28.0 m/s · sin 22.0° -9.80 m/s² · 3.77 s

vy = -26.5 m/s

v = (26.0 m/s, -26.5 m/s)

The magnitude of v will be:

`|v| = \sqrt{(26.0 m/s)^(2) + (26.5 m/s)^(2)}=37.1 m/s`

Again, when you do not round any intermediate result, the speed is the same for the three balls:

The velocity of ball C will be 37.0 m/s

Then:

speed ball A = speed ball B = speed ball C = 37.0 m/s