Answer:
C) may experience a magnetic force, but its speed will not change.
Step-by-step explanation:
When a charged particle is moving in a static uniform magnetic field, it experiences a force whose magnitude is
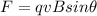
where
q is the charge
v is the velocity of the charge
B is the strength of the magnetic field
 is the angle between the directions of v and B
is the angle between the directions of v and B
Also, the direction of the force is perpendicular to both v and B.
Using these information, we can make the following observations:
- The particle does not experience a force when the velocity v is parallel to the field (because
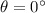 ), so option A) is wrong
), so option A) is wrong
- The direction of the force is perpendicular to v, so the force does not do any work on the particle: this means that the particle's speed does not change, so option B) is wrong as well
- Finally, option D) is wrong as well, because the direction of the force is perpendicular to v, so it makes the direction of the particle changing (in fact, the particle will follow a circular motion)
Summarizing all these observations, we finally conclude that option C) is correct, since the particle may experience a magnetic force, but its speed will not change