Question

The area of a rectangle fountain is (x^2 + 12x + 20) square feet. A 2-foot walkway is built around the fountain. Find the dimensions of the outside border of the walkway.

Answer 1

Length=x+14 ft

Width=x+6 ft

Explanation:

Step 1

Information provided

`Area = x^(2)+12x+20`

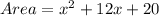
Step 2

By factorization

`Area = x^(2)+2x+10x+20`

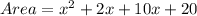
Area=x(x+2)+10(x+2)

Notice that x+2 are common on RHS therefore,

Area=(x+2)(x+10)

Since the length is usually longer than width, then x+10 is taken as original length, x+2 is the original width.

Step 3

When a 2-ft walkway is built, dimensions of outside border increase by 2ft+2ft=4ft

Therefore, length=x+10+4=x+14 ft

Width=x+2+4=x+6 ft

Ans

Length=x+14 ft

Width=x+6 ft