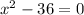Answer:
The equation that has solutions 6 and -6 is
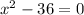
Solution:
We have to find which equation has the solutions 6 and -6.
We have been given three equations.
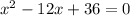 --- eqn 1
--- eqn 1
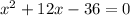 -- eqn 2
-- eqn 2
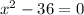 ---- eqn 3
---- eqn 3
The 6 and -6 to satisfy any of these equations they have to be the roots of the equation.
This means that when we substitute 6 and -6 in any of the equations and then solve them the answer on simplification should be 0.
This condition should individually be satisfied by both 6 and -6 for any one of the equations.
Now let us try and substitute 6 and -6 in eq1.
Now, substituting 6 in eq1.
62-12×6+36=0
Now we simply the equation to check is the LHS is equal to the RHS of the equation.
LHS:
72-72=0
RHS: 0
Since LHS=RHS it is the root of the equation.
Now we check if -6 satisfies eq1.
-62-12×-6+36=0
LHS:
72+72=144
RHS: 0
Hence LHS is not equal to RHS, -6 is not the root of eq1.
Similarly we check for eq2
Checking for 6 and -6 we get
LHS is not equal to RHS hence this does not satisfy eq2.
Now in the same way we check for eq3
LHS=RHS for both 6 and -6 hence they are the solutions for eq3.
Hence the equation that has solutions 6 and -6 is