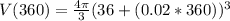Question

A high-altitude spherical weather balloon expands as it rises, due to the drop in atmospheric pressure. Suppose that the radius r increases at the rate of 0.02 inches per second, and that r = 36 inches at time t = 0. Determine the equation that models the volume V of the balloon at time t, and find the volume when t = 360 seconds.

V(t) = 4π(0.02t)2; 651.44 in3

V(t) = 4π(36 + 0.02t)2; 1,694,397.14 in3

V(t) = four pi times the product of zero point zero two and t to the third power divided by three.; 4,690.37 in3

V(t) = four pi times the quantity of thirty six plus zero point zero two t to the third power divided by three.; 337,706.83 in3

Answer 1

V(t)=
`(4\pi )/(3) (36+0.02t)^(3)`

337 706, 83
`in^(3)`

Explanation:

The volume of a sphere is
`V=(4\pi )/(3) r^(3)`

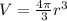
So like the initial radius is 36 and is increasing of 0.02 every second, we define the radius:

r= 36+0.02t

So, we replace in the formula of the volume and we obtain

`V(t)= (4\pi )/(3) (36+0.02t)^(3)`

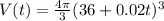
and if we replace t= 360 seconds in the equation of volume, we get

`V(360)= (4\pi )/(3) (36+(0.02*360))^(3)`

`V(360)=337 706, 83 in^(3)`