Answer:
a) 2.8% of products exhibit edge roughness.
b) If a paper has rough edges, there is an 8.93% probability that it was slit by a new knife blades.
c) If it has rough edges, there is a 91.07% probability that it was slit with a blade of average sharpness blades or worn blades.
Explanation:
We have these following probabilities:
A 25% probability that the blade is new
A 60% probability that the blade is of average sharpness.
A 15% probability that the blade is worn.
If a blade is new, a 1% probability that it has rough edges.
If a blade is of average sharpness, a 3% probability it has rough edges.
If a blade is worn, a 5% probability it has rough edges.
a. What is the proportion of products that exhibit edge roughness?
This is
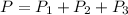
 are those that are new and exhibit edge roughness. So
are those that are new and exhibit edge roughness. So
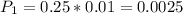
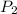 are those of average sharpness that exhibit rough edges. So
are those of average sharpness that exhibit rough edges. So

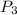 are those that are worn and exhibit rough edges. So
are those that are worn and exhibit rough edges. So
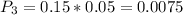
So
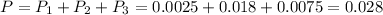
2.8% of products exhibit edge roughness.
b. If a paper was selected at random and found that it has rough edges, what is the probability that it was slit by a new knife blades?
From a), we found that there is a 0.028 probability that it has rough edges.
Also, there is a 0.0025 probability that it was slit by a new knife blades and have rough edges. So
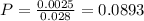
If a paper has rough edges, there is an 8.93% probability that it was slit by a new knife blades.
c) If a paper was selected at random and found that it has rough edges, what is the probability that it was slit with a blade of average sharpness blades or worn blades
From a), we found that there is a 0.028 probability that it has rough edges.
Also, there is a 0.018 probability that it was sliced with a blade of average sharpness and has rough edges and an 0.0075 probability that it was slices with worn blades and has rough edges. So

If it has rough edges, there is a 91.07% probability that it was slit with a blade of average sharpness blades or worn blades.