Question

Between t = 0 and t = t0, a rocket moves straight upward with an acceleration given by a(t)=A−Bt1/2a(t)=A−Bt1/2 , where A and B are constants. (a) If x is in meters and t is in seconds, what are the units of A and B? (b) If the rocket starts from rest, how does the velocity vary between t = 0 and t = t0? (c) If its initial position is zero, what is the rocket’s position as a function of time during this same time interval?

Answer 1

a) A = [m /s²] , B = [m /
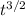`t^(3/2)`] , b) v = a to + 2B/3
`t^(3/2)`

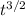
Step-by-step explanation:

a) to define the units of the constants, we see that the left part has units of acceleration so the right part must also have the same units

A = [m /s²]

B = [m / s²]

B = [m /
`t^(3/2)`]

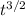b) We must use the definition of acceleration

a = dv / dt

dv = adt

We integrate

∫ dv = ∫ (A + B
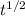`t^(1/2)`) dt

v = a t + B 2/3
`t^(3/2)`

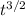
We evaluate between:

the lower limit t = 0 v = o and the upper limit t = to v = v

v = a to + 2B/3
`t^(3/2)`

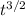
c) Let's use the definition of speed

v = dx / dt

dx = v dt

∫ dx = ∫ (a t + 2B/3
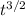`t^(3/2)`) dt

x = a t²/2 + 2b/3 2/5
`t^(5/2)`

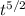
For the interval t = 0 and t = to, we evaluate the integral

x = A/2 t₀² + 4B/15 √t₀⁵