Question

In the short run, a firm cannot vary its capital, K=2, but can vary its labor, L. It produces output q. Explain why the firm will or will not experience diminishing marginal returns to labor in the short run if its production function is. A) q=10L + K and B) q= L^0.5 K^0.5

Answer 1

A) no, the quantity increases at a constant rate.

B) yes, quantity increases at a lower rate after each additional units of labor is added.

Step-by-step explanation:

We should derivate to know if the function increases or decreases:

at until which point this occur:

A)

q = 10 L + K

if K = 2

q = 10L +2

q' = 10

As q' is positive and constant the function increases at the same rate for all the positives values of L.

B)

`q = 2^(0.5) * L^(0.5)`

`q' = (0.5* 2^(0.5))L^(-0.5)`

`q' = ((0.5* 2^(0.5)))/(√(L))`

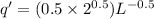
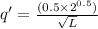
As L increases, the additional output decreases. This economy faces diminishing marginal returns to labor.