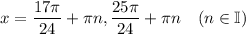Answer:
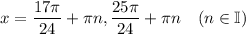
Explanation:
Given the cosine equation:
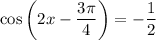
Let:
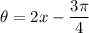
Then we will have:
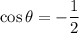
We know that cosθ is negative in second quadrant and third quadrant.
In second quadrant:
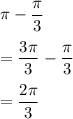
In third quadrant:
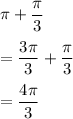
Therefore, we will have two solutions where:
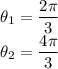
Convert from theta back to the original expression:
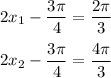
Convert two equations into one:
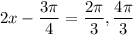
Since you do not specify the interval, add
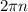 where
where
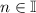 .
.
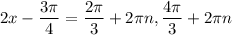
Solve the equation for x:
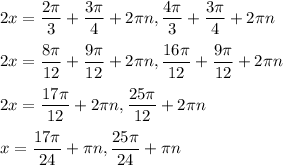
Therefore, the solution is: