Question

Use the drawing tools to form the correct answer on the number line.

Graph the solution set to this inequality.
31 – 11 > 71 + 9

Answer 1

We conclude that

`3x-11>7x+9\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<-5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-5\right)\end{bmatrix}`

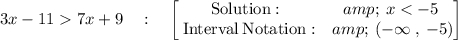
Please check the attached diagram which shows the solution on the number line.

Explanation:

Given the inequality

`3x-11>7x+9`

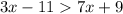
Add 11 to both sides

`3x-11+11>7x+9+11`

Simplify

`3x>7x+20`

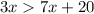
Subtract 7 from both sides

`3x-7x>7x+20-7x`

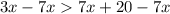
Simplify

`-4x>20`

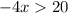
Multiply both sides by -1 (reverses the inequality)

`\left(-4x\right)\left(-1\right)<20\left(-1\right)`

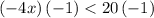
Simplify

`4x<-20`

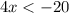
Divide both sides by 4

`(4x)/(4)<(-20)/(4)`

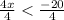
Simplify

`x<-5`

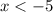
Therefore, we conclude that

`3x-11>7x+9\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<-5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-5\right)\end{bmatrix}`

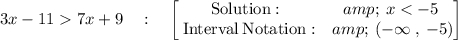
Please check the attached diagram which shows the solution on the number line.