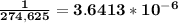Answer:
a) 274,625
b)
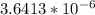
Explanation:
a)
We have an arrangement of 3 numbers (p,q,r) each of them having 65 different possible selections.
By the Fundamental Rule of Counting, there are
65*65*65 = 274,625 different combinations.
b)
Since there is a unique combination which unlocks the device, the probability of guessing it at the first try is