Answer:
 = 19.32 m/s and
= 19.32 m/s and
 = 27.32 m/s
= 27.32 m/s
Step-by-step explanation:
The kinetic energy has as formula
K = ½ m v²
Where m is the mass and v the speed of the body.
If the policeman calculates the kinetic energy, let's clear the speed
v = √ 2K/m
Let's reduce the units to the SI system
K = 16.32 KJ (1000 J / kJ) = 16.32 10³ J
Let's calculate
v = RA (2 16.32 10 3/60)
v = 23.32 m / s
The rider at 14.4 km/h, reduce
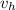 = 14.4 km / h (1000m / 1km) (1h / 3600s) = 4.00 m / s
= 14.4 km / h (1000m / 1km) (1h / 3600s) = 4.00 m / s
We already have the relative speed of the two (rider and police car) which is 23.32, we also have the rider speed 4.0 m / s, let's calculate the possible police speeds
These two speeds come from going in the same direction or in opposite directions
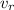 =
=
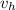 ±
±
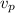
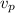 =
=
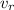 - vj
- vj
 = 23.32 - 4
= 23.32 - 4
 = 19.32 m/s
= 19.32 m/s
 =
=
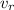 + vj
+ vj
 = 23.32 +4
= 23.32 +4
 = 27.32 m/s
= 27.32 m/s