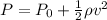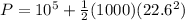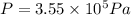Question

Your town is installing a fountain in the main square. If the water is to rise 26.0 m (85.3 feet) above the fountain, how much pressure must the water have as it moves slowly toward the nozzle that sprays it up into the air? Assume atmospheric pressure equal to 100,000. Pa and g=9.81 m/s2.

Answer 1

`P = 3.55 * 10^5 Pa`

Step-by-step explanation:

As we know that water from the fountain will raise to maximum height

`H = 26.0 m`

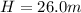
now by energy conservation we can say that initial speed of the water just after it moves out will be

`(1)/(2)mv^2 = mgH`

`v = √(2gH)`

`v = √(2(9.81)(26))`

`v = 22.6 m/s`

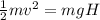
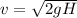
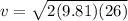
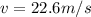
Now we can use Bernuolli's theorem to find the initial pressure inside the pipe

`P = P_0 + (1)/(2)\rho v^2`

`P = 10^5 + (1)/(2)(1000)(22.6^2)`

`P = 3.55 * 10^5 Pa`