Question

You and your friend throw balloons filled with water from the roof of a several story apartment house. You simply drop a balloon from rest. A second balloon is thrown downward by your friend 2.2 s later with an initial speed of 43.12 m/s. They hit the ground simultaneously. How high is the apartment house? The acceleration of gravity is 9.8 m/s 2 . Neglect air resistance. Answer in units of m.

Answer 1

Height = 53.361 m

Step-by-step explanation:

There are two balloons being thrown down, one with initial speed (u1) = 0 and the other with initial speed (u2) = 43.12

From the given information we make the following summary

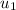`u_(1)` = 0m/s

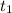`t_(1)` = t

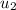`u_(2)` = 43.12m/s

`t_(2)` = (t-2.2)s

The distance by the first balloon is

`D = u_(1) t_(1)  + (1)/(2) at_(1)^2`

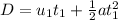
where

a = 9.8m/s2

Inputting the values

`D = (0)t + (1)/(2) (9.8)t^2\\ D = 4.9t^2`

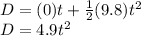
The distance traveled by the second balloon

`D = u_(2) t_(2)  + (1)/(2) at_(2)^2`

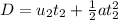
Inputting the values

`D = (43.12)(t-2.2)  + (1)/(2) (9.8)(t-2.2)^2`

simplifying

`D = 4.9t^2 + 21.56t -71.148`

Substituting D of the first balloon into the D of the second balloon and solving

`4.9t^2 = 4.9t^2 + 21.56t -71.148 \\ 21.56t = 71.148\\ t = 3.3s`

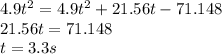
Now we know the value of t. We input this into the equation of the first balloon the to get height of the apartment

`D = 4.9(3.3)^2\\ D = 53.361 m`