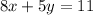Question

Find the equation of the line.

Through (2, -1); parallel to the line 8x + 5y = 6
Which of the following is the equation of the line in standard form?

Answer 1

`8x + 5y = 11`

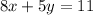
Explanation:

First, to obtain the gradient we must rearrange the equation into the form
`y = mx + b`, where
`m` is the gradient and
`b` is the y-intercept (the point where the line crosses the y-axis).

To rearrange to this form, take away
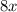`8x` from both sides and divide by 5:

`y =  -(8)/(5)x + (6)/(5)`

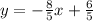
From this equation, we can see the gradient is
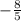`-(8)/(5)` and the y-intercept is
`(6)/(5)`

Now, to obtain the equation of the line parallel to
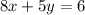`8x + 5y = 6` we must find the new y-intercept. To do this, rearrange
`y = mx + b` to find
`b`.

`b = y - mx`

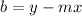
We know the value of
`m` from above (
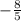`-(8)/(5)`), and the coordinates the line must pass through are in the question (2, -1).

We just put those values into the equation and solve for
`b`:

`b = y - mx = (-1) - (- (8)/(5) )(2) = (16-5)/(5) = (11)/(5)`

Now, rearrange back to the original form and you obtain the answer:

`8x + 5y = 11`