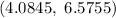Question

A university with a high water bill is interested in estimating the mean amount of time that students spend in the shower each day. In a sample of 11 students, the average time was 5.33 minutes and the standard deviation was 1.33 minutes. Using this sample information, construct a 99% confidence interval for the mean amount of time that students spend in the shower each day. Assume normality.

Answer 1

Answer:
`(4.0845,\ 6.5755)`

Explanation:

As per given , we have

n = 11

`\overline{x}=5.33\\\\ s=1.33`

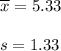
Since population standard deviation is missing, so we use t-test.

Critical t-value for 99% confidence :

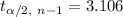`t_(\alpha/2,\ n-1)=3.106` [using two-tailed t-value table]

Confidence interval :

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))\\\\= 5.33\pm (3.1060)(1.33)/(√(11))\\\\\approx5.33\pm1.2455\\\\=(5.33-1.2455,\ 5.33+1.2455)\\\\=(4.0845,\ 6.5755)`

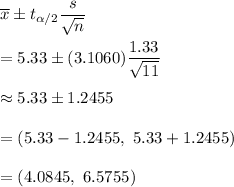
Hence, 99% confidence interval for the mean amount of time that students spend in the shower each day.=
`(4.0845,\ 6.5755)`