Question

A line passes through the points (-1, -2) and (2, 7). Answer the following questions about the line:

Part A: Find the slope of the line.
Part B: Using the slope from Part A, find the y-intercept of the line.
Part C: Using the slope from Part A and the y-intercept from Part B, write an equation for the line in slope-intercept form.
Part D: Convert the equation from the slope-intercept form (Part C) to standard form.

Answer 1

A. Slope = 3

B. y-intercept = 1

C. Slope-Intercept Form is y = 3x + 1

D. Standard Form is -3x + y = 1

Explanation:

A.

Given two points
`(x_1, y_1)` and
`(x_2,y_2)`, we define the slope as:

Slope =
`(y_2-y_1)/(x_2-x_1)`

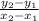
This is the rate of change of a function (line).

Given the two points, we find the slope to be:

`(y_2-y_1)/(x_2-x_1)\\=(7-(-2))/(2-(-1))\\=(7+2)/(2+1)\\=(9)/(3)\\=3`

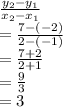
Thus,

The slope is 3

B.

Slope-Intercept form of a line is y = mx + b

Where m is slope and b is the y-intercept

We plug in 3 into m, and use one point given (such as (2,7) and place 2 into x and 7 into y, and solve for b (the y-intercept). Shown below:

`y=mx+b\\7=3(2)+b\\7=6+b\\b=7-6\\b=1`

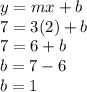
Hence y-intercept is 1

C.

The slope intercept form of a line is y = mx + b

Where m is the slope

b is the y -intercept (the place in graph where the line cuts the y-axis)

Now, we know m = 3 (from A)

and b = 1 (from B)

Now, we put these into the slope-intercept form of a line and get the equation as:

y = mx + b

y = 3x + 1

D.

The standard form of a line is given by Ax + By = C

So we need to keep the x and y on the left side and take the constant to the right side. Let's convert slope intercept form (from part C) to standard form:

y = 3x + 1

-3x + y = 1