Answer:
v_{f} = -0.693 m / s
Step-by-step explanation:
The acceleration of the runner can be obtained from Newton's second law
F = m a
a = F / m
the bold are vectors, therefore the acceleration throughout the journey varies as the force has variations.
For the part of finding the velocity of the body we can use the relationship between the momentum and the variation of the momentum
I = Δp
∫ F Δt = m
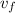 - m v₀
- m v₀
int F dt = m (v_{f}-v₀)
1) To find the change in velocity we must find the area under the curve of the graph, this can be done analytically if we know the functional of the curve or approximate it by intervals
a) between 0 <t <0.20 s
v) between 0.20 <t <0.30 s
a reasonable curve shape can be a Gaussian.
2) If we do not have the form of the cure, we can perform a graphical integration to find the area under the curve, we can do this by dividing the curve into small rectangles, finding the area of each one and adding them.
3) Another even more approximate way is to create an average force in each interval and find the area of this force, the average force is the average value of the force in the interval, let's use this method in the exercise
a) first interval 0 <t <0.20 Average force
 = 300 N
= 300 N
area = F_{mean} Δt
area = I = 300 0.20
I = 60 N s
the speed change is
I = m Δv
Δv = I / m
Δv = 60/65
Δv = 0.923 m / s
If we assume that the runner starts from rest, his final velocity is v = 0.923 m / s in the direction of the force.
b) second interval 0.2 <t <0.30s average force F_mean = 150 N
area = I = 150 (0.30 - 0.20)
I = 15 N s
the speed change is
Δv = 15/65
Δv = 0.23 m / s
Note that in this case the initial speed is not zero and since the two impulses are in the opposite direction the speed decreases
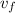 = -0.923 + 0.23
= -0.923 + 0.23
v_{f} = -0.693 m / s