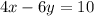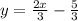Question

Find all solutions of the given system of equations (If the system is infinite many solution, express your answer in terms of x) a) 2x-3y 3 14x 6y 3 Noot 4x- 6y 10 16x- 24y 40 b)

Answer 1

(a) The system of the equations
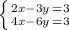`\left \{ {2x-3y\:=3} \atop {4x-6y\:=3}} \right.` has no solution.

(b) The system of the equations
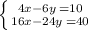`\left \{ {4x-6y\:=10} \atop {16x-24y\:=40}} \right.` has many solutions
`y=(2x)/(3)-(5)/(3)`

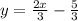
Explanation:

(a) To find the solutions of the following system of equations
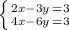`\left \{ {2x-3y\:=3} \atop {4x-6y\:=3}} \right.` you must:

Multiply
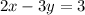`2x-3y=3` by 2:

`\begin{bmatrix}4x-6y=6\\ 4x-6y=3\end{bmatrix}`

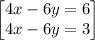
Subtract the equations

`4x-6y=3\\-\\4x-6y=6\\------\\0=-3`

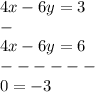
0 = -3 is false, therefore the system of the equations has no solution.

(b) To find the solutions of the system
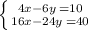`\left \{ {4x-6y\:=10} \atop {16x-24y\:=40}} \right.` you must:

Isolate x for
`4x-6y=10`

`x=(5+3y)/(2)`

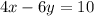
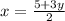
Substitute
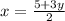`x=(5+3y)/(2)` into the second equation

`16\cdot (5+3y)/(2)-24y=40\\8\left(3y+5\right)-24y=40\\24y+40-24y=40\\40=40`

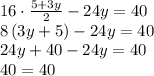
The system has many solutions.

Isolate y for
`4x-6y=10`

`y=(2x)/(3)-(5)/(3)`