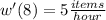Question

Find the equation of the tangent line to the curve when x has the given value.

14) f(x) = -2- x2; x = -1



15) According to one theory of learning, the number of items, w(t), that a person can learn

after t hours of instruction is given by:

w(t) = 15
`\sqrt[3]{t^2}` 0 ≤ t ≤ 64

Find the rate of learning at the end of eight hours of instruction.

Answer 1

14) The equation of the tangent line to the curve
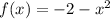`f(x)=-2-x^2` at x = -1 is
`y=2x-1`

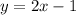
15) The rate of learning at the end of eight hours of instruction is
`w'(8) = 5 (items)/(hour)`

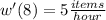
Explanation:

14) To find the equation of a tangent line to a curve at an indicated point you must:

1. Find the first derivative of f(x)

`f(x)=-2-x^2\\\\(d)/(dx) f(x)=(d)/(dx)(-2-x^2)\\\\\mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g'\\\\(d)/(dx) f(x)=(d)/(dx)\left(-2\right)-(d)/(dx)\left(x^2\right)\\\\f'(x)=-2x`

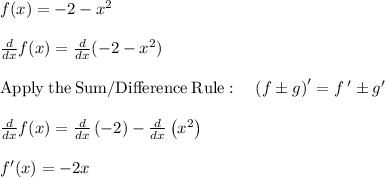
2. Plug x value of the indicated point, x = -1, into f '(x) to find the slope at x.

`f'(-1)=-2(-1)=2`

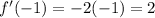
3. Plug x value into f(x) to find the y coordinate of the tangent point

`f(-1)=-2-(-1)^2=-3`

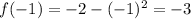
4. Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line

`y-y_1=m(x-x_1)\\y+3=2(x+1)\\y=2x-1`

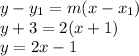
5. Graph your function and the equation of the tangent line to check the results.

15) To find the rate of learning at the end of eight hours of instruction you must:

1. Find the first derivative of f(x)

`w(t)=15\sqrt[3]{t^2} \\\\(d)/(dt)w= (d)/(dt)(15\sqrt[3]{t^2})\\\\w'(t)=15(d)/(dt)\left(\sqrt[3]{t^2}\right)\\\\\mathrm{Apply\:the\:chain\:rule}:\quad (df\left(u\right))/(dx)=(df)/(du)\cdot (du)/(dx)\\\\f=\sqrt[3]{u},\:\:u=\left(t^2\right)\\\\w'(t)=15(d)/(du)\left(\sqrt[3]{u}\right)(d)/(dt)\left(t^2\right)\\\\w'(t)=15\cdot \frac{1}{3u^{(2)/(3)}}\cdot \:2t\\\\\mathrm{Substitute\:back}\:u=\left(t^2\right)`

`w'(t)=15\cdot \frac{1}{3(t^2)^{(2)/(3)}}\cdot \:2t\\w'(t)=\frac{10t}{\left(t^2\right)^{(2)/(3)}}`

2. Evaluate the derivative a t = 8

`w'(t)=\frac{10t}{\left(t^2\right)^{(2)/(3)}}\\\\w'(8)=\frac{10\cdot 8}{\left(8^2\right)^{(2)/(3)}}\\\\=\frac{80}{\left(8^2\right)^{(2)/(3)}}\\\\\left(8^2\right)^{(2)/(3)}=16\\\\=(80)/(16)\\\\w'(8) = 5 (items)/(hour)`

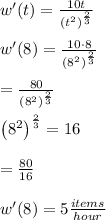
The rate of learning at the end of eight hours of instruction is
`w'(8) = 5 (items)/(hour)`