Question

(Car Sales) Of the cars sold during the month of July, 94 had air conditioning, 96 had automatic transmission, and 80 had power steering. 6 cars had all three of these extras. 18 cars had none of these extras. 21 cars had only air conditioning, 62 cars had only automatic transmissions, and 25 cars had only power steering. 11 cars had both automatic transmission and power steering. How many cars had air conditioning and automatic transmission but not power steering?a) 23b) 44c) 29d) 6e) 5f) None of the above.

Answer 1

56

Explanation:

Answer 2

18 cars had air conditioning and automatic transmission but not power steering.

Explanation:

To solve this problem, we must build the Venn's Diagram of these sets.

I am going to say that:

-The set A represents the cars that had air conditioning.

-The set B represents the cars that had automatic transmission.

-The set C represents the cars that had power steering.

-The value of d represents the cars that had none of those extras.

We have that:

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

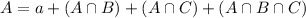
In which a is the number of cars that only had air conditioning,
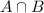`A \cap B` is the number of cars that have both air conditioning and automatic transmission,
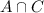`A \cap C` is the number of cars that have both air conditioning and power steering. And
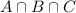`A \cap B \cap C` is the number of cars that had all those three extras.

By the same logic, we have:

`B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)`

`C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)`

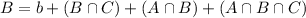
How many cars had air conditioning and automatic transmission but not power steering?

This is
`A \cap B`.

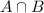We start finding the values from the intersection of three sets

6 cars had all three of these extras. This means that

`A \cap B \cap C = 6`

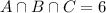
11 cars had both automatic transmission and power steering.

This is

`(B \cap C) + (A \cap B \cap C) = 11`

`(B \cap C) = 5`

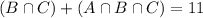
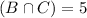
25 cars had only power steering.

This means that
`c = 25`

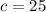
62 cars had only automatic transmissions.

This means that
`b = 62`.

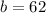21 cars had only air conditioning

This means that
`a = 21`

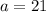
80 had power steering

This means that
`C = 80`

`C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)`

`80 = 25 + (A \cap C) + 5 + 6`

`A \cap C = 44`

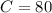
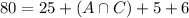
Now, we can use the equation of A or B to find
`A \cap B`

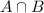
96 had automatic transmission. This means that
`B = 96`

`B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)`

`96 = 62 + 5 + (A \cap B) + 11`

`(A \cap B) = 18`

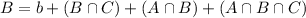
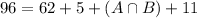
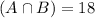
18 cars had air conditioning and automatic transmission but not power steering.