Question

determine the value of x that the line containing (3,4) and (8,-6) is perpendicular to the line containing (2,4) and (x,3)

Answer 1

x = 0

Explanation:

The critical information we need to know here is that:

"the product of the slopes of 2 lines that are perpendicular is -1"

So we need to find the slope of each and multiply them and equate it to -1 and solve for x. First, we need to find the slope.

Slope is given by the formula:

`(y_2-y_1)/(x_2-x_1)`

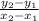
Where

x_1 and x_2 are the x coordinates of the points respectively, and

y_1 and y_2 are the y coordinates of the points respectively.

First, the slope of (3,4) and (8,-6) using formula above:

`(-6-4)/(8-3)=(-10)/(5)=-2`

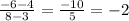
Secondly, the expression for slope of (2,4) and (x,3) using same formula:

`(3-4)/(x-2)=(-1)/(x-2)`

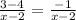
Now we multiply both and equate to -1 and solve for x:

`(-1)/(x-2)*(-2)=-1\\(2)/(x-2)=-1\\2=-1(x-2)\\2=-x+2\\x=2-2\\x=0`

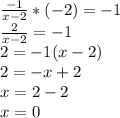
Thus, the value of x is 0