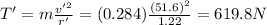Question

A string under a tension of 50.4 N is used to whirl a rock in a horizontal circle of radius 2.51 m at a speed of 21.1 m/s. The string is pulled in and the speed of the rock increases. When the string is 1.22 m long and the speed of the rock is 51.6 m/s, the string breaks. What is the breaking strength (in newtons) of the string?

Answer 1

619.8 N

Step-by-step explanation:

The tension in the string provides the centripetal force that keeps the rock in circular motion, so we can write:

`T=m(v^2)/(r)`

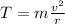
where

T is the tension

m is the mass of the rock

v is the speed

r is the radius of the circular path

At the beginning,

T = 50.4 N

v = 21.1 m/s

r = 2.51 m

So we can use the equation to find the mass of the rock:

`m=(Tr)/(v^2)=((50.4)(2.51))/(21.1^2)=0.284 kg`

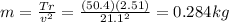
Later, the radius of the string is decreased to

r' = 1.22 m

While the speed is increased to

v' = 51.6 m/s

Substituting these new data into the equation, we find the tension at which the string breaks:

`T'=m(v'^2)/(r')=(0.284)((51.6)^2)/(1.22)=619.8 N`