Answer:
A and C
Explanation:
Rewriting for the sake of clarity:
Select all radical expressions that are equivalent to
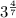
![a)(\sqrt[7]{3^(4)})\\b)\sqrt[4]{21}\\c)\sqrt[7]{81}\\d)\sqrt[4]{3^(7)}\\e)\sqrt[7]{12}\\f)\sqrt[4]{3^(7)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zrshwwlyhb4525iub9da4smebgcgukx9vq.png)
1) According to the Exponents Law, when we have a fraction as an exponent the numerator of it will be the radicand's exponent and the denominator will be the index of it.
![3^{(4)/(7)}=(\sqrt[7]{3^(4)})](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fo3gccsy79ifn6yy9861ddqsj8qxb26vt9.png)
2) We can raise the 3 to the 4th power. And rewrite the radicand as the result of that:
![3^{(4)/(7)}=\sqrt[7]{3^(4)}=\sqrt[4]{21}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qv1k4eaflcwszd4y2bfanbc48fukng86lp.png)