(a) 0.714 cm
First of all, we need to find the spring constant of the spring. This can be done by using Hooke's law:
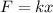
where
F is the force applied on the spring
k is the spring constant
x is the stretching of the spring
At the beginning, the force applied is the weight of the block of m = 4.20 kg hanging on the spring, therefore:
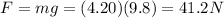
The stretching of the spring due to this force is
x = 2.00 cm = 0.02 m
Therefore, the spring constant is
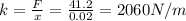
Now, a new object of 1.50 kg is hanging on the spring instead of the previous one. So, the weight of this object is
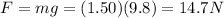
And so, the stretching of th spring in this case is
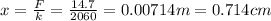
(b) 1.65 J
The work done on a spring is given by:
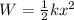
where
k is the spring constant
x is the stretching of the spring
In this situation,
k = 2060 N/m
x = 4.00 cm = 0.04 m is the stretching due to the external agent
So, the work done is
