Answer:
The value of f(1) is smaller than the value of f(3)
Explanation:
The correct question is
Given the function f(x) = 2x^2 + 3x + 10, find f(1) and f(3). Choose the statement that is true concerning these two values.
The value of f(1) is the same as the value of f(3).
The value of f(1) cannot be compared to the value of f(3).
The value of f(1) is larger than the value of f(3).
The value of f(1) is smaller than the value of f(3)
we have
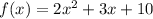
step 1
Find out the value of f(1)
substitute the value of x=1 in the function f(x)
so
For x=1
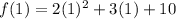
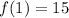
step 2
Find out the value of f(3)
substitute the value of x=3 in the function f(x)
so
For x=3
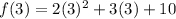
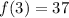
step 3
Compare the values
37> 15
so
f(3) > f(1)
or
f(1) < f(3)
therefore
The value of f(1) is smaller than the value of f(3)