Let
 with
with
 be the lower right vertex of the rectangle, so its base has total length
be the lower right vertex of the rectangle, so its base has total length
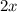 . The height of the rectangle will be the function value this value of
. The height of the rectangle will be the function value this value of
 , or
, or
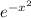 .
.
Then the area of the rectangle is
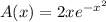
Differentiate
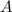 with respect to
with respect to
 and find the critical points.
and find the critical points.
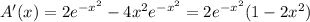
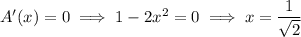
Evaluate the second derivative at this critical point to ensure
 is maximized there.
is maximized there.
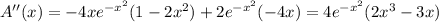
Since
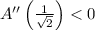 , this is indeed a local maximum. Then the largest area is
, this is indeed a local maximum. Then the largest area is
