Question

The sequence follows a times -1 pattern: 6, -6, 6, -6. Write a formula for the (n)th term of the sequence. Your “n” term must start with 1

Answer 1

The formula for the nth term of the sequence is:

`a_n=a_1\cdot r^(n-1)`

Explanation:

Given the sequence

6, -6, 6, -6

A geometric sequence has a constant ratio r and is defined by

`a_n=a_1\cdot r^(n-1)`

Computing the ratios of all the terms of the adjacent terms

`(-6)/(6)=-1,\:\quad (6)/(-6)=-1,\:\quad (-6)/(6)=-1`

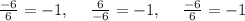
The ratio of all the adjacent terms is the same and equal

so

r = -1

so substituting r = -1 and
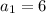`a_1=6` in the geometric sequence

`a_n=a_1\cdot r^(n-1)`

`a_n=6\left(-1\right)^(n-1)`

Thus, the formula for the nth term of the sequence is:

`a_n=a_1\cdot r^(n-1)`