Question

Item 10 The height y (in feet) of an arrow t seconds after it is shot from a bow can be modeled by the function y=−16t2+80t + 6. a. Write the function in vertex form. y= b. Find the maximum height of the arrow. The maximum height of the arrow is feet. c. How long does it take the arrow to hit the ground? Round your answer to the nearest second. It takes about seconds for the arrow to hit the ground.

Answer 1

Part a) The function in vertex form is
`y=-16(t-2.5)^(2)+106`

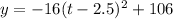
Part b) The maximum height of the arrow is 106 feet

Part c) It takes about 5 seconds for the arrow to hit the ground

Explanation:

we have

`y=-16t^(2)+80t+6`

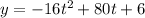
where

y ----> is the height (in feet) of an arrow

t ----> is the time in seconds after it is shot from a bow

This is the equation of a vertical parabola open downward

The vertex is a maximum

Part a) Part b) Write the function in vertex form. Find the maximum height of the arrow

we have

`y=-16t^(2)+80t+6`

Factor -16

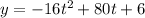
`y=-16(t^(2)-5t)+6`

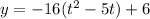
Complete the squares

`y=-16(t^(2)-5t+6.25)+6+100`

`y=-16(t^(2)-5t+6.25)+106`

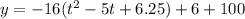
Rewrite as perfect squares

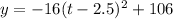`y=-16(t-2.5)^(2)+106` ----> equation in vertex form

The vertex is the point (2.5,106)

The maximum height of the arrow represent the y-coordinate of the vertex of the function

therefore

The maximum height of the arrow is 106 feet

Part c) How long does it take the arrow to hit the ground?

we know that

When the arrow hit the ground the value of y is equal to zero

so

For y=0

`0=-16(t-2.5)^(2)+106`

`16(t-2.5)^(2)=106`

`(t-2.5)^(2)=(106)/(16)`

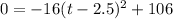
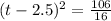
take square root both sides

`(t-2.5)=(+/-)(√(106))/(4)`

`t=2.5(+/-)(√(106))/(4)`

`t=2.5(+)(√(106))/(4)=5\ sec`

`t=2.5(-)(√(106))/(4)=-0.07\ sec`

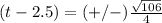
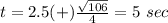
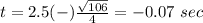
therefore

It takes about 5 seconds for the arrow to hit the ground