Answer:

Explanation:
A sequence is given to us is , and we need to find expression for nth term of the sequence. The given sequence is ,
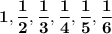
When we flip the numbers , we can clearly see that the number are in Harmonic Progression.
That is when we flip the numbers they are found to be in Arithmetic Progression .
And nth term of an Harmonic Progression is :-

Hence here
- Common difference = 1
- First term = 1 .
Substituting the respective values,
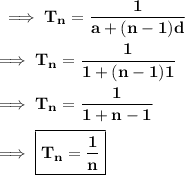
Hence the nth term of the given sequence is given by ¹/n .