Question

A researcher wishes to conduct a study of the color preferences of new car buyers. Suppose that 50% of this population prefers the color brown. If 15 buyers are randomly selected, what is the probability that more than a third of the buyers would prefer brown? Round your answer to four decimal places.

Answer 1

The probability that more than a third of the buyers would prefer brown is 0.8491.

Explanation:

This is binomial problem with n=15 and p=0.50.

The binomial formula of probaility is:

P(X=x)=
`(n!)/(x!(n-x)!) p^(x) (1-p)^(n-x)`

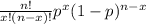
More than a third of the buyers: 15÷3=5

We have to find P(x>5).

P(x>5) = 1 - P(x≤5) = 1 - P(x=0) - P(x=1) - P(x=2) - P(x=3) - P(x=4) - P(x=5)

P(x=0)=
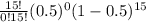`(15!)/(0!15!) (0.5)^(0) (1-0.5)^(15)`=0.00003

P(x=1)=
`(15!)/(1!14!) (0.5)^(1) (1-0.5)^(14)`=0.00046

P(x=2)=
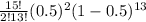`(15!)/(2!13!) (0.5)^(2) (1-0.5)^(13)`=0.00320

P(x=3)=
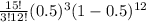`(15!)/(3!12!) (0.5)^(3) (1-0.5)^(12)`=0.01389

P(x=4)=
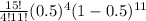`(15!)/(4!11!) (0.5)^(4) (1-0.5)^(11)`=0.04165

P(x=5)=
`(15!)/(5!10!) (0.5)^(5) (1-0.5)^(10)`=0.09164

P(x>5) = 1 - P(x≤5)= 1- 0.00003 - 0.00046 - 0.00320 - 0.01389 - 0.04165 - 0.09164 = 0.8491