Question

A baseball player at second base throws a ball 90 feet to the player at first base. The ball is released at a point 5 feet above the ground with an initial velocity of 50 miles per hour and at an angle of 15° above the horizontal. At what height does the player at first base catch the ball? (Round your answer to three decimal places.)

Answer 1

The height is 1.498 meters.

Explanation:

In order to find the height, you have to apply the equations of Projectil Motion.

-For the x-axis:

Xf=Xo+Vox.t (I)

Where Xf is the final position, Xo is the initial position, Vox is the horizontal component of velocity and t is the time.

-For the y-axis:

Yf=Yo+Voy.t-0.5gt² (II)

Where Yf is the final position, Yo is the initial position, Voy is the vertical component of velocity, t is the time and g is the acceleration of gravity (9.8 m/s²).

The initial velocity in m/s is:

`(50(milles)/(hour))((1hour)/(3600s))((1meter)/(0.0006milles))=23.148m/s`

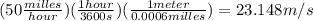
You have to calculate the horizontal and vertical components of the initial velocity. The velocity vector forms a right triangle with an angle of 15° with the horizontal, therefore you can obtain the components applying trigonometric identities.

Vox= 23.148(m/s)Cos(15°)=22.359 m/s

Voy=23.148(m/s)Sin(15°)=5.991 m/s

Using (I) to obtain the time when the horizontal position of the ball is 90 feet

90 feet in m/s is:

`90feet((0.3048meters)/(feet))=27.432m`

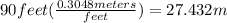
27.432=0+22.359t

Dividing by 22.359:

t=1.227 s.

Replacing the time in (II) to obtain the final vertical position of the ball:

The initial vertical position in meters is:

`5feet((0.3048meters)/(feet))=1.524 m`

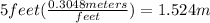
Yf = 1.524 + 5.991(1.227)-0.5(9.8)(1.227)²

Yf= 1.498 j m (where j is the unit vector in the y-axis)

Which is the height where the player catches the ball.