Answer:
337 reserved seats & 582 general admission seats were sold
Explanation:
Let the number of general admission be g, and
the number of reserved seats be r
Since $2 costs general and $4.5 costs reserved and in total $2680.50, we can write an equation as:
2g + 4.5r = 2680.5
Also, in total there are 919 general and reserved seats. Thus, we can write 2nd equation as:
g + r = 919
Rearranging, we get:
g = 919 - r
We put this into first equation (to get all in r) and solve for r first:
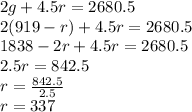
And now, since we know g = 919 - r, we have:
g = 919 - r
g = 919 - 337 = 582
Thus, 337 reserved seats & 582 general admission seats were sold