Question

2 lines intersect. Where the 2 lines intersect, 4 angles are created. Labeled clockwise, from uppercase right: angle 1 (3 x minus 1) degrees, angle 2 is blank, angle 3 (2 x + 9) degrees, and angle 4 is blank.

What are the numerical measures of each angle in the diagram?
∠1 and ∠3 measure degrees.
∠2 and ∠4 measure degrees

Answer 1

∠1 and ∠3 measure 29 degrees

∠2 and ∠4 measure 151 degrees

Explanation:

Answer 2

∠1 and ∠3 measure 29 degrees

∠2 and ∠4 measure 151 degrees

Explanation:

we know that

Vertical angles are a pair of opposite angles formed by intersecting lines. They are always congruent to one another

see the attached figure to better understand the problem

we have that

m∠1=m∠3 -----> by vertical angles

m∠2=m∠4 -----> by vertical angles

m∠1+m∠2=180° ----> by supplementary angles (form a linear pair)

m∠3+m∠4=180° ----> by supplementary angles (form a linear pair)

In this problem we have

m∠1=(3x-1)°

m∠3=(2x+9)°

substitute in the expression

m∠1=m∠3

`(3x-1)\°=(2x+9)\°`

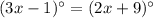
Solve for x

`3x-2x=9+1`

`x=10`

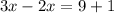
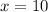
Find the measure of m∠1

m∠1=(3x-1)°

substitute the value of x

m∠1=(3(10)-1)=29°

Find the measure of m∠3

Remember that

m∠3=m∠1

therefore

m∠3=29°

Find the measure of m∠2

we have that

m∠1+m∠2=180°

m∠1=29°

substitute

29°+m∠2=180°

m∠2=180°-29°=151°

Find the measure of m∠4

Remember that

m∠4=m∠2

therefore

m∠4=151°

therefore

∠1 and ∠3 measure 29 degrees

∠2 and ∠4 measure 151 degrees